Простыми словами про волновое электричество

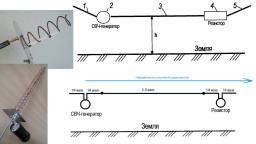
Волновая природа электричества - это вам не унылая квантовая физика, хотя и в ней есть относительно неплохо квантующееся волновое электричество, но оно какое-то не такое. Надо более простыми словами, чтобы было понятно даже детям.

Во Горчилина понесло! Слава начинает простыми словами, но звучит интригующе для физмата:

«В начале было Слово,
и Слово было у Бога…»
Евангелие от Иоанна

Введение

Уважаемые читатели, мы рады представить вашему вниманию волновую теорию электричества, которая, без сомнения, будет сначала принята научным сообществом в штыки, так как заявляет о полностью волновой природе любой частицы, при этом её корпускулярная природа является лишь следствием изначального постулата.

Науке уже давно известно, что все механические взаимодействия прежде всего — электрические. Это следует хотя-бы из того, что они осуществляются между электронными оболочками атомов.

Прим. от издателя: Здесь меня подбросило, и я захотел прокричать матом, но на Славу не буду. У него симуляторы на сайте классные. Трудяга. Мне такое программирование не осилить.

Квантовая механика оперирует понятием волновой функции, которая показывает лишь плотность вероятности нахождения электрона в атоме, т.е. где электрон размазан по пространству наиболее вероятно. Уже отсюда получается, что как таковой частицы и нет, а все взаимодействия в природе осуществляются только лишь за счёт волновых процессов.

Ну правильна, раз электрона нет, надо притянуть что-нибудь другое. А не проще ли выкинуть электронно-протонное из атома вообще? Нет не проще. Проще даже бросить науку.

В этой работе будет показан общий принцип взаимодействий между частицами (их волнами), которые всегда стремяться занять наивыгоднейшее энергетическое положение, находись они в связанном состоянии в атоме или же — будучи свободны. Это приведёт нас к наиболее общему закону взаимодействий, включающему закон Кулона, закон всемирного тяготения и другие известные закономерности.

Караул! Попахивает электрической гравитацией. И граблями по лбу: бам, бам, бамс.

Отсюда, как следствие такого взаимодействия, не привлекая дополнительные постулаты, мы получим квантованность энергии и импульса.

Это то, о чем я мечтал! Квантовать и еще раз квантовать! Но лимит на научные дерзости в этом материале исчерпан и я замолкаю.

Несмотря на заявленную нами волновую природу элементарных частиц, в этой работе мы будем использовать их названия для упрощения восприятия, например — электрон и протон. Но при этом, всегда будем подразумевать их волновую функцию, которую представим далее.

Здесь мы будем иметь дело больше не с массами и зарядами, а с волнами, их амплитудами и фазами. А поскольку стоячая волна практически всегда будет распределённой в пространстве, то — и с её узлами и пучностями [1].

На данном этапе этой теории будет рассмотрена 2D пространственная модель, причём вторая координата будет образовываться за счёт мнимой части выражений. Например, импульс будет записываться без знака вектора, но на самом деле подразумевается, что это — двумерный математический объект. Вообще говоря, комплексное число — это способ одномерной записи двумерного пространства [2], которого нам будет вполне достаточно для построения всех необходимых выводов. О трёх- и четырёх- мерном пространстве будут лишь сделаны некоторые предположения.

Еще одно первоначальное допущение, которое должно сильно упростить восприятие материала, это рассмотрение исключительно водородоподобных атомов [3] и взаимодействий в них. Несмотря на это, теория окажется вполне работоспособна и в других случаях.

1.1 Модель волнового электрона и протона

В начале, для удобства, ведём относительный радиус x, который будет отсчитываться от геометрического центра частицы x=r/r0 (1.1)

Здесь: r0 — боровский радиус [4]. Обозначим относительные амплитуды электрона и протона

A e (x) = N e x exp [i (π x / N e - π / 4)] (1.2)

A p (x) = N p x exp [i (π x / N p + 3 π / 4)] (1.3)

Здесь введены следующие обозначения: N^e,N^p — число электронов и протонов соответственно. Вообще говоря, будем следовать правилу, при котором нижний индекс будет обозначать номер частицы или номер группы частиц, а верхний — её класс (электрон, протон).

Из формул хорошо видно, что фаза волны протона сдвинута от электронной на 180 градусов (или на

π). На самом деле, в показателе степени этих формул потребуются ещё дополнительный угол, связанный с небольшой несимметрией этих частиц. Он появится во второй части этой работы, а поскольку этот угол очень маленький, то на данном этапе мы им пренебрежём.

Чтобы более наглядно представить, что из себя представляют эти функции, мы можем составить параметрический график, где по оси ординат отразим её действительные значения, а по оси абсцисс — мнимые. Но будет ещё понятнее, если такие функции представить в нормированном виде, когда

N^e=N^p=1, т.е. когда мы описываем один электрон и один протон. Они отражены на рисунках 1 и 2 в виде раскручивающихся спиралей, сдвинутых относительно друг друга на 180 градусов.

Рис.1. Параметрический график приведенной волновой функции электрона

Рис.2. Параметрический график приведенной волновой функции протона

Таким образом получается, что частицы создают вокруг себя некоторые всепроникающие поля в виде волн, при этом саму частицу, как вещество, в таком контексте можно более не рассматривать. Свойства этого поля мы будем раскрывать по мере развития этой теории, но на данный момент понятно, что оно не должно экранироваться. Необходимо также придумать ему название, например, грави-поле или G-поле. Электрические, магнитные и гравитационные поля будут являться лишь разными формами его проявления, при определённых условиях.

Дальше даю ссылку: https://gorchilin.com/articles/wave-electricity/wel. Наслаждайтесь примером когда математика дискредитирует физику.