Фотонов нет, а вы не знали? Тогда статья доктора Гришаева вам понравится. Увы нашу земную физику сотворили идиоты, а голоса достойных ученых в этом мире мало кому интересны.
У нас же физику учат не для того, чтобы знать как устроен мир, а для чисто меркантильных целей.
Раздел 3. ПРИРОДА СВЕТА
3.1. Как начиналась сказка про фотоны.
Некоторые древнегреческие философы учили, что мы видим глазами потому, что из глаз выходят тончайшие щупальца, которыми мы ощупываем предметы на расстоянии. Эта концепция, в рамках тогдашних знаний о мире, выглядела вполне правдоподобно. А рухнула она от простенького возражения – попробуйте, мол, что-нибудь вот так ощупать в совершенно тёмной комнате! Не получается? То-то же. Пришлось допустить, что мы можем видеть глазами предметы тогда, когда в глаза попадает нечто, идущее от предметов. Это нечто и есть свет. В тёмной комнате света нет, поэтому там – «хоть глаз выколи».
История развития научных представлений о природе света – это история углубления научного бессилия. Ибо чем больше появлялось опытных данных про свет, тем становилось всё яснее, что научные представления о нём – никуда не годные.
Ньютон представлял свет как поток корпускул. Первые же измерения скорости света показали, что световые корпускулы должны летать с огромной скоростью. Представляете, как они сталкивались бы при пересечениях курсов, и как при этом они изменяли бы направления полёта! Однако, лучи зрения множества наблюдателей могут пересекаться, и при этом каждый наблюдатель успешно видит свой объект. Такое может быть, по Ломоносову, если свет – это не поток корпускул, а волны в какой-то особой среде. Ведь для волн как раз характерно – проходить друг сквозь друга без взаимных помех! Но лишь когда у света обнаружились дифракция и интерференция – лишь тогда волновая теория стала господствующей. Пришлось придумать среду – световой эфир – где распространявшиеся механические колебания и представляли собой световые волны. Ох, и намучились физики, пытаясь построить модель эфира. Ведь эфир должен был обеспечивать механические колебания на оптических частотах, которые распространялись бы с огромной скоростью – скоростью света! Для механических колебательных систем эти цифры – совершенно запредельные. Хуже того: уравнения Максвелла, которые изначально описывали механические колебания в эфире – и давали, в качестве решения, распространяющиеся волны – были, по сути, уравнениями сплошной среды. Однако, сплошных сред в природе не бывает, да и механические колебания возможны в тех средах, которые состоят из отдельных частичек, связанных силами упругости. Но самые большие трудности из-за концепции эфира возникли в оптике движущихся тел. Считалось, что эфир заполняет всё мировое пространство, будучи однороден, изотропен и неподвижен. А скорость упругих волн в среде определяется только свойствами этой среды, поэтому волна движется с характеристической скоростью по отношению к местному участку среды. Казалось бы, экспериментатор на Земле, вектор скорости которой по отношению к эфиру изменяется (из-за годичного обращения), мог бы обнаружить соответствующие вариации скорости света. Но, увы… Были предложены модели, в которых эфир движущимися телами увлекался – частично или полностью. Всё тщетно. Ни одна модель эфира не объясняла всей совокупности экспериментальных фактов. Наконец, с подачи Эйнштейна, эфир упразднили. Но уравнения Максвелла сохранили, поскольку на их лорентц-инвариантности и держалось всё то, что называлось «теорией относительности». Раньше уравнения Максвелла описывали волны в среде, а теперь они стали «описывать» волны в чистом поле, без всякой среды. Откуда там, в чистом поле, берутся возвращающие силы, необходимые для наличия и распространения колебаний (кстати, колебаний чего?) – науке это до сих пор не ведомо. Причём, когда это всё начиналось, было уже хорошо известно, что характеристические спектры атомов представляют собой наборы отдельных линий. Считалось, что каждой такой линии соответствует своя волна, которая излучается при механических осцилляциях электрона в атоме – на резонансной частоте.
И вот произошли два свершения. Второе из них: Резерфорд предложил планетарную модель атома. Основания для этой модели были, но, согласно ей, электроны в атоме осциллировали постоянно, поскольку они обращались вокруг ядра. А, значит, постоянно порождали световые волны. А, значит, постоянно теряли энергию. И, стремительно падая по спирали на ядро, успевали бы излучить широченный спектр – вместо отдельных линий, наблюдавшихся на опыте… А, несколько ранее этого свершения, Планку удалось соорудить математическое выражение, описывавшее спектр равновесного излучения, у которого максимум при комнатной температуре находится в инфракрасной области. Тут, правда, не обошлось без надувательства. Смотрите: выражение для электромагнитного спектра можно записать так, чтобы аргументом являлась частота – а можно так, чтобы аргументом являлась длина волны. Планк предложил оба эти варианта [П1,П2]. Казалось бы, это два выражения для одного и того же спектра. Но, поразительным образом, их максимумы сильно не совпадают. Чтобы в этом убедиться, следует взять производные от этих выражений и, приравняв их нулю, найти положения максимумов, а затем привести результаты к какой-нибудь одной физической величине – например, к энергии, удачно выражаемой в единицах kT, где k - постоянная Больцмана, а T - абсолютная температура. И окажется, что максимум длин-волнового выражения Планка соответствует энергии 4.97kT, а максимум частотного выражения Планка – энергии 2.82kT [Г1]. Не мы первые это обнаружили: вопрос обсуждался даже на академическом уровне [Г2,С1,Г3]. Авторы предлагали «промежуточный» вариант выражения для равновесного спектра – с однозначным максимумом. Но, увы, этот вариант не находился в согласии с опытом: на опыте блестяще подтверждалось длин-волновое выражение Планка [Б1,Л1]. А в чём же тогда было надувательство? А в том, что всю квантовую теорию, со всеми её далеко идущими следствиями, строили на частотном выражении Планка, которое на опыте не подтверждалось!
И вот, в этом выражении, не подтверждаемом на опыте, фигурировало произведение частоты на подгоночный множитель, которому впоследствии присвоили статус фундаментальной константы – постоянной Планка. Произведение конкретной частоты на эту постоянную давало конкретную порцию энергии. Вот же они, кванты света! Ух, как они пригодились, чтобы решить проблему с устойчивостью атомов, которая возникала в планетарной модели Резерфорда! Бор, не напрягаясь, всё разъяснил: у атомарного электрона, мол, есть набор стационарных орбит, по которым он обращается, не излучая. А излучение-поглощение – квантами! – происходит, мол, при переходах с одной стационарной орбиты на другую. Эти переходы, мол, и дают наблюдаемые линейчатые спектры! Всё хорошо, но почему электрон, обращаясь по стационарной орбите, не излучает? Да, получается, потому, что Бор так постулировал!
Знаете, зависимость энергии кванта света только от частоты – это поначалу людей с ума сводило. Ведь квант света представляли как отрезочек электромагнитной волны. Сколько же периодов колебаний укладывается на этом отрезочке? Казалось бы: вдвое больше число колебаний – вдвое больше и энергия. Ан нет, при одной и той же частоте, квант длиной в одно колебание и квант длиной в миллион колебаний должны иметь одинаковую энергию! И, если частота является единственным параметром, определяющим энергию кванта, то что колеблется с этой частотой в атоме, поглотившем этот квант? И сколько длится «акт испускания» кванта атомом, тот самый переход электрона с орбиты на орбиту? Отчаявшись найти разумные ответы на эти вопросы, физики на Первом Сольвеевском конгрессе приняли постановление о том, что квант излучается и поглощается мгновенно. Так оно, конечно, спокойнее – если забыть про то, что этот «отрезочек волны» движется со скоростью света, и что он должен иметь какую-никакую длину. Ведь этот вопрос – насчёт длины кванта – на редкость мутный. Вот, например, фемтосекундный лазер. Длина светового импульса длительностью 100 фемтосекунд – 30 микрон. А вот другой пример – узкополосный лазер на красителе фирмы «Coherent Radiation». При ширине его спектра всего в 15 кГц, эквивалентная длина когерентности составляет 3 км. Какова же длина кванта света, если она – то не более 30 микрон, то не менее 3 км? Кстати, если квант света имел бы длину 30 микрон, то как он мог бы лететь в прозрачном твёрдом теле от атома к атому, если расстояние между ними составляет несколько Ангстрем? Вы, дорогой читатель, представляете, как от атома к атому может лететь нечто, имеющее длину на пять порядков больше, чем расстояние между ними? Не получается? Ну, ладно, тогда про 3-километровый квант лучше и не вспоминать…
Впрочем, это всё можно назвать лёгкими недоразумениями по сравнению с центральным догматом квантовой теории – согласно которому, атом может поглощать и излучать только такие кванты света, энергии которых в точности равны разностям энергий атомарного электрона на тех самых стационарных орбитах. Как такое можно было сморозить? Ведь у атомов различных химических элементов различны и наборы квантовых уровней энергии, соответствующих «стационарным орбитам». Выходит, что без специальных мер – сдвигающих или уширяющих квантовые уровни – квант света, излучённый атомом одного элемента, не может быть поглощён атомом другого элемента. Позвольте, если бы так оно и было, то электромагнитное взаимодействие не было бы универсальным! Вот эти атомы обменивались бы только такими квантами, а вон те – другими! Но, к счастью, таких глупостей в мироустройстве нет – известно множество свидетельств о том, что атомы способны поглощать и излучать не только резонансные световые кванты, соответствующие разностям энергий квантовых уровней в атоме, но и нерезонансные кванты, соответствующие континууму между квантовыми уровнями. Первое из этих свидетельств было известно с самого рождения квантовой теории – это спектр равновесного излучения, который, как известно, сплошной. А нам пытаются вдолбить, что атом может поглотить-излучить лишь дискретные порции энергии! Если бы это было так, то атомы не могли бы быть источниками равновесного излучения – а, значит, не могли бы участвовать в равновесном радиационном теплообмене! Но это вопиющее противоречие квантовой теории с тем, чему нас учит термодинамика, не образумило теоретиков – они, наверное, думали, что со временем это всё забудется, и тогда придёт полное понимание. Отнюдь: со временем появились ещё и экспериментальные опровержения центрального догмата квантовой теории. Например, вопреки квантовой теории, заработали лазеры. В первых лазерах использовалась накачка импульсными широкополосными лампами-вспышками. Атомы рабочего тела поглощали нерезонансные кванты накачки, после чего скатывались на верхний уровень лазерного перехода. Известно, далее, о флуоресценции веществ в результате их облучения заведомо нерезонансным ультрафиолетом: она происходит на длине волны, в точности соответствующей разности энергий нерезонансного кванта облучения и энергии нижерасположенного квантового уровня в облучаемом веществе. Наконец, в современной лазерной спектроскопии активно развиваются направления, в которых поглощение-излучение атомами нерезонансных квантов рассматривается уже как нечто само собой разумеющееся. Речь идёт о генерации суммарной частоты, а также о разнообразных методиках многофотонной спектроскопии (см. обзорную монографию [Д1]). В физическом жаргоне появился термин «виртуальный уровень» – это на нём, на виртуальном уровне, оказывается атом при поглощении нерезонансного кванта (к вопросу о континууме энергий между стационарными уровнями мы вернёмся в 5.1). Но, несмотря на перечисленные потрясающие успехи экспериментаторов, никто официально не отменил запрета квантовой теории на поглощение-излучение атомами нерезонансных квантов.
А почему так? А потому что тронь центральный догмат квантовой теории – и вся эта гнилая конструкция рухнет, ибо она изначально строилась не неверных предпосылках. Главной из этих неверных предпосылок является тезис о том, что кванты света – или, как их стали называть впоследствии, фотоны – являются порциями энергии, которые существуют самостоятельно, независимо от атомов, которые их излучают и поглощают. Однако, по логике «цифрового мира», обладателем физических энергий, в самых различных формах, является только вещество (1.1). Световая энергия не является исключением: она тоже локализована только на атомах. При распространении света она не проходит по разделяющему атомы пространству: энергия возбуждения перебрасывается – на расстояние! – непосредственно с атома на атом. О квантовых перебросах этой энергии мы будем подробно говорить ниже (3.4). Как нам представляется, все попытки физиков построить сколько-нибудь разумную и непротиворечивую модель фотона провалились по одной простой причине: никаких фотонов, в традиционном понимании, не существует. А ведь фотон, как считается, входит в четвёрку фундаментальных, абсолютно стабильных частиц! Но мы покажем, что потуги выдать фотон за реальную частицу – через приписывание фотону свойств реальных частиц – являлись либо заведомой ложью, либо неверной интерпретацией опытных фактов. И вначале мы разберёмся – чего стоят «доказательства» того, что фотоны переносят импульс.
3.2. Где же доказательства того, что фотоны переносят импульс?
Первым и весьма наглядным свидетельством о том, что световая энергия передаётся порциями, стало явление фотоэффекта – вылета электронов из металлической пластинки, облучаемой ультрафиолетом. Если бы энергия облучения падала на пластинку «волнами», то энергии фотоэлектронов увеличивались бы по мере увеличения интенсивности облучения. Однако, энергии фотоэлектронов увеличивались лишь по мере уменьшения длины волны облучения. «Это потому, - разъяснил Эйнштейн, - что каждый фотоэлектрон выбивается одним квантом света, энергия которого и превращается в кинетическую энергию электрона – за вычетом потери на работу выхода из пластинки». Впрочем, «выбивается» - это сильно сказано. Фотоэлектроны вылетали из освещённой стороны пластинки – словно их только припекло, но не пнуло! Они вылетали в направлении, противоположном направлению полёта «выбивавших» их квантов света! Как это получалось, даже Эйнштейн объяснить не брался. О законе сохранения энергии здесь можно было говорить уверенно, а вот о законе сохранения импульса… Ну, да чёрт с ним. Для Нобелевской премии и этого хватило!
А уж как хотелось получить свидетельства о том, что кванты света переносят не только энергию, но и импульс! Вон, чем ближе комета к Солнцу, тем сильнее её ядро «пылит и газит», и тем сильнее это пыле-газовое облако (кома) «сметается» в направлении от Солнца – отчего у кометы формируется хвост. Считается, что Кеплер первый высказал в 1619 г. гипотезу о том, что «сметающим» фактором, формирующим хвосты комет, является давление светового излучения Солнца. Впоследствии электромагнитная теория света Максвелла привела к выводу о том, что давление света прямо пропорционально световой энергии, ортогонально падающей на площадку в единицу времени. Например, для давления, оказываемого солнечными лучами на радиусе орбиты Земли, на основе величины солнечной постоянной, ≈1400 Вт/м2, получается величина около 5?10-6 н/м2. Лебедев утверждал [Л2], что именно давление солнечного света формирует хвосты комет, но соответствующих расчётов он не привёл – для таких расчётов требовалось знать множество параметров пыле-газовых облаков комет, а этими знаниями наука тогда не располагала.
Сегодня, когда наука такими знаниями располагает, всё так же необоснованно считается, что давление солнечного света является основным фактором, формирующим хвосты комет. Между тем, сегодня известно о потоке плазмы от Солнца – солнечном ветре – частицы которого, несомненно, переносят импульс. При средних значениях параметров солнечного ветра на радиусе орбиты Земли, т.е. при концентрации частиц, равной 10 протонам в 1 см3, и их скоростях, равных 500 км/c [Ф1], для давления солнечного ветра получаем величину ≈4.3?10-9 н/м2. Это на три порядка меньше величины светового давления, полученной на основе солнечной постоянной (см. выше) – и, казалось бы, говорить о действии солнечного ветра применительно к хвостам комет неуместно, поскольку здесь световое давление явно доминирует. Однако, такой подход не учитывает одно важное обстоятельство. А именно: солнечная постоянная характеризует излучение в широком сплошном спектре. Молекулы же газов, из которых состоит кома кометы, рассеивают лишь то излучение (в видимом диапазоне), которое попадает на полосы поглощения. Если учесть этот селектирующий фактор, то доминирующим оказывается действие солнечного ветра [Г4]. Причём, вопрос о том, какое из двух давлений – солнечного света или солнечного ветра – формирует хвосты комет, без особых проблем мог быть разрешён астрономическими наблюдениями. Известно, что в годы активного Солнца солнечный световой поток, практически, постоянен, а вот интенсивность солнечного ветра возрастает на порядок. Значит, если хвосты комет формируются давлением солнечного света, то заметной разницы у хвостов комет при спокойном и активном Солнце не наблюдалось бы, а если они формируются давлением солнечного ветра – разница наблюдалась бы. О недостатке объектов для наблюдения говорить не приходится: «Ежегодно наблюдается около десятка комет. Из них… 4-5 наблюдавшихся ранее, причём об их повторном появлении известно заранее. Две кометы – Швассмана-Вахмана и Отерма – наблюдаются ежегодно» [С2]. Тем не менее, нам удалось найти лишь одно свидетельство по данному вопросу: «Немецкий астроном Бирманн недавно выдвинул предположение, что солнечное корпускулярное излучение, т.е. частицы, вылетающие из Солнца с большими скоростями, тоже могут играть важную роль; он нашёл подтверждение своей теории в изучении влияния солнечных магнитных бурь на комету Уиппла-Федтке» [С3]. Одного этого свидетельства достаточно для вывода о том, что хвосты комет формируются, главным образом, под действием солнечного ветра – и, таким образом, хвосты комет не могут служить доказательством наличия светового давления.
А обнаруживается ли давление света в лаборатории? Считается, что оно обнаружилось в опытах Лебедева [Л3]. В этих опытах свет от электрической дуги направлялся на мишени из фольги, прикреплённые к крылышкам лёгких крутильных маятников разных конструкций. За время освещения с одной стороны, маятнику давали совершить одно полное колебание, замечая при этом три положения максимальных отклонений – по которым вычисляли нулевое положение. Затем свет направляли с другой стороны, и точно так же находили новое нулевое положение. Половина разности между этими двумя нулевыми положениями, как полагали, соответствовала силовому эффекту от светового давления.
Но главным фактором, маскировавшим искомый эффект, являлись радиометрические силы [Л3]. Эти силы обусловлены тем, что, в прилегающем к мишени объёме, температура газа с освещённой стороны выше, чем с неосвещённой – что порождает соответствующую разницу давлений на мишень. Радиометрические силы в значительной степени ослаблялись вакуумированием баллона, в котором помещался крутильный маятник; но полностью эти силы, конечно, не устранялись. Вызывает недоумение тот факт, что величину ожидаемого эффекта из-за действия этих сил – для реальных условий опыта – автор не привёл. Тогда не могло ли оказаться, что этими силами был обусловлен весь наблюдаемый эффект?
В пользу этого подозрения мы усматриваем одно важное свидетельство. Согласно теории Максвелла, давление света зависит от коэффициента отражения поверхности, на которую падает свет: для абсолютно отражающей поверхности давление в два раза больше, чем для абсолютно поглощающей. Поэтому Лебедев и использовал два типа мишеней: сильно поглощающих, покрытых платиновой чернью – и сильно отражающих, имевших зеркальное напыление. Но, вместо ожидавшейся почти двукратной разницы, имело место лишь незначительное превышение наблюдаемого эффекта для зеркальных мишеней по сравнению с чернёными. На основе рядов данных в [Л3], которые имеет смысл сравнивать, т.е. полученных для одного и того же маятника и одного и того же калориметра, измерявшего падавшую энергию, мы получили следующие средние величины эффекта (в условных единицах):
маятник N2 – (чернь) 1.55±0.07, (зеркала) 1.89±0.31;
маятник N3 – (чернь) 1.30±0.18, (зеркала) 1.70±0.24.
Как можно видеть, для маятника N2 отношение средних величин эффектов для чернённых и зеркальных мишеней составило всего-то 1.2, а для маятника N3 – 1.3. Эти цифры говорят о том, что Лебедев имел дело не с давлением света, а, скорее всего, с остаточными радиометрическими силами.
Весьма показательно и следующее обстоятельство. Спустя десятилетия, опыты Лебедева могли быть повторены в условиях, гораздо более благоприятных для устранения радиометрических сил. В баллоне Лебедева давление остаточных газов было несколько ниже, чем 10-4 мм.рт.ст. [Л3]. Для сравнения: при поточном производстве радиоламп, их колбы откачивали до давления 10-7 мм.рт.ст. [Е1], а в экспериментальных технических установках достигается давление ещё на несколько порядков ниже. Кроме того, могли быть использованы лазерные источники света, которые не только давали бы гораздо более мощный, чем у Лебедева, поток световой энергии, но и, при подходящем выборе рабочей длины волны, практически исключали бы действие света на остаточные газы. Однако, про сообщения о подобных опытах нам неизвестно. Трудно поверить в то, что никто не пытался ставить эти опыты. Проще поверить в то, что, после устранения радиометрических сил, пропадал и наблюдаемый силовой эффект. А чтобы публика-дура об этом не догадалась, придумали игрушку с замечательным названием: «радиометрическая вертушка». Светишь на её крыльчатку, а она и вертится! «Пусть вас не смущает название вертушки, - разъяснили публике, - она вертится из-за давления света!»
И вот, поскольку упорно не доказывался перенос импульса фотонами, когда они летели потоком, оставалась надежда лишь на доказательства переноса импульса отдельным фотоном. Считается, что первым таким доказательством стал эффект Комптона. Этот эффект заключается в рассеянии веществом рентгеновского излучения – с характерным увеличением его длины волны. Классическая теория рассеяния света не смогла объяснить этот феномен, и было принято объяснение Комптона [К1], основанное на подходе квантовой теории.
Согласно этому объяснению, рентгеновский фотон неупруго соударяется со слабо связанным атомарным электроном. При этом, как следует из законов сохранения энергии и импульса, часть своей энергии (и импульса) фотон передаёт электрону, выбивая его из атома и превращая в «электрон отдачи». В результате, как следует из законов сохранения энергии-импульса, длина волны фотона увеличивается. Такой подход согласуется с главными свойствами комптоновского сдвига длины волны: во-первых, с его независимостью от атомного номера вещества рассеивателя и, во-вторых, с его зависимостью лишь от угла, на который происходит рассеяние.
Однако, ради торжества подхода Комптона был проигнорирован ряд особенностей, с которыми этот подход не согласуется. Следует иметь в виду, что комптоновский сдвиг длины волны потому и заметен с помощью спектрометров, что в рассеянном на любой угол излучении присутствует также несмещённая компонента – с той же самой длиной волны, что и у падающего излучения. Если законы сохранения энергии-импульса дают, при рассеянии фотона на ненулевой угол, ненулевой комптоновский сдвиг длины волны, то неужели несмещённая компонента порождается с нарушением этих законов? Теоретики пытаются убедить нас в том, что несмещённая компонента порождается при таком соударении фотона с атомарным электроном, при котором электрон не выбивается из атома, т.е. фотон соударяется, фактически, не с электроном, а с атомом – а поскольку масса атома гораздо больше массы электрона, то импульс отдачи у атома оказывается ничтожен. Тогда теоретикам следовало бы объяснить, отчего фотон с энергией, которая на 3 порядка больше энергии связи атомарного электрона, в одних случаях выбивает электрон из атома, а в других случаях не выбивает – рассеиваясь при этом на один и тот же угол. Увы, разумного объяснения этому нет. Далее, не удаётся наблюдать комптоновское рассеяние на атомах сверхлёгких (в частности, водорода) и тяжёлых элементов – хотя свойства слабо связанных электронов у всех элементов ничем принципиально не различаются. Наконец, уничтожающим доводом против подхода Комптона является тот малоизвестный факт, что в рассеянном на любой угол излучении присутствует, помимо комптоновской и несмещённой компонент, ещё и компонента анти-комптоновская – длина волны которой уменьшена на величину комптоновского сдвига [С6]. В теорию Комптона совершенно не укладывалось наличие анти-комптоновской компоненты, поэтому он в известных нам публикациях даже не упоминал про неё.
Мы же, в работе [Г5], предлагаем более адекватное и честное объяснение феномена. Согласно нашей модели, рассеяние рентгеновских лучей здесь происходит не на атомарных электронах, а на нуклонных комплексах в ядрах – и при этом сдвиги длин волн зависят от «электронного» пространственного размера, от его комптоновской длины волны! Наша модель не только легко объясняет возможность всех трёх компонент: комптоновской, несмещённой и анти-комптоновской. Мы объясняем, почему эффект Комптона не наблюдается при рассеянии рентгеновских лучей на атомах сверхлёгких элементов, например, на водороде – у водорода нет требуемых для этого нуклонных комплексов. Мы объясняем, почему эффект Комптона не наблюдается при рассеянии рентгеновских лучей на атомах тяжёлых элементов – хотя эти атомы, конечно, тоже имеют «слабо связанные» электроны. Разгадка здесь, на наш взгляд, в том, что рентгеновские кванты эффективно взаимодействуют с электронами из внутренних электронных оболочек тяжёлых атомов – отчего эти кванты попросту «не добираются» до ядер. Наконец, мы объясняем, почему эффект Комптона не наблюдается для видимого света – хотя, согласно логике квантовой теории рассеяния, комптоновские сдвиги здесь вполне могли бы иметь место, а их наблюдение не представляло бы особых технических сложностей. Разгадка в том, что видимый-то свет рассеивается именно атомарными электронами, а не нуклонными комплексами в ядрах.
И ещё: в отличие от модели Комптона, которая требует наличия выбиваемых из атомов «электронов отдачи», по нашей модели, никаких «электронов отдачи» не существует. А ведь был проведён целый ряд экспериментов [Ш3,Х1,К2], призванных подкрепить шаткие представления Комптона и проиллюстрировать разлёт продуктов комптоновского рассеяния – при котором рассеянный квант и «электрон отдачи» вылетают из атома одновременно и разлетаются под «правильными» углами. В работе [Г5] дан критический обзор подобных экспериментов, и показана их полная бездоказательность. Их общим недостатком было отсутствие доказательств того, что исследовалось именно комптоновское рассеяние – измерением комптоновских сдвигов здесь никто себя не утруждал. Впрочем, в некоторых «подтверждающих» опытах использовали в качестве первичного излучения гамма-кванты [Х1,К2], у которых измерять комптоновские сдвиги было просто нечем [Г5]. Так, Крэйн, Гартнер и Турин [К2] поместили мишень-рассеиватель в центре камеры Вильсона – для проверки того, что направления вылета электрона отдачи и рассеянного фотона находятся в согласии с законами сохранения энергии-импульса. В качестве первичного излучения использовались жёсткие гамма-лучи – что делало весьма сомнительной саму возможность комптоновского рассеяния. Электроны, которые, судя по их трекам, вылетали из мишени вперёд, считались электронами отдачи – хотя они могли быть электронами внутренней конверсии или фотоэлектронами, выбиваемыми вторичными гамма-квантами. Поскольку гамма-квант не оставляет трека в камере Вильсона, то, для подтверждения «правильного» направления полёта рассеянного гамма-кванта, требовалось получить «правильные» фотографии. А именно: на них, помимо трека «электрона отдачи», требовалось зафиксировать, в «правильном» сегменте камеры, трек ещё одного электрона – якобы, выбитого рассеянным гамма-квантом. Мы говорим «якобы», поскольку никаких гарантий того, что второй электрон выбивался гамма-квантом, вылетавшим из мишени в центре камеры, быть не могло. При таком положении дел, «правильная» пара треков могла получаться лишь в результате маловероятного стечения случайных обстоятельств, на ничтожном проценте фотографий – как это и было в действительности. Обработав только эти «удачные» фотографии, авторы сделали неизбежный, при подобном высоконаучном подходе, вывод о том, что «наблюдаемый угол полёта рассеянного фотона совпадает с вычисленным» [Ш1]. Вот такой лепет нам подсовывают в качестве подпорок заявлений Комптона – насчёт того, что фотон переносит импульс! Добавим, что скептические слова в адрес традиционной интерпретации комптоновских сдвигов, а также критические замечания по поводу экспериментов с «электронами отдачи» высказывались и ранее – например, в исследовании [А1].
Ещё одним эффектом, который, как полагают, доказывает перенос импульса гамма-квантом, является эффект Мёссбауэра. До открытия Мёссбауэра, наблюдение резонансного ядерного поглощения было затруднено – как считалось, из-за эффекта отдачи: гамма-квант, якобы, передаёт часть своего импульса как излучающему его ядру, так и поглощающему, отчего их совпадающие невозмущённые линии «разъезжаются» из-за эффекта Допплера. Это объяснение – недоразумение какое-то. Допплеровский сдвиг линии излучателя имеет место, когда соответствующая скорость у излучателя уже имеется. В рассматриваемом же случае эта скорость приобретается в результате отдачи, т.е. после того, как излучение гамма-кванта уже произошло. Аналогично, у ядра-поглотителя допплеровский сдвиг линии, из-за эффекта отдачи, мог бы появиться лишь после того, как уже произошло поглощение. Ну, никак не мог эффект отдачи портить резонансное ядерное поглощение! Но нам предъявляют факты: при сближении излучателя и поглотителя, вероятность этого поглощения увеличивалась. Казалось бы, здесь происходила допплеровская компенсация эффекта отдачи. И, когда Мёссбауэр обнаружил резонансное поглощение при отсутствии допплеровской компенсации, а при условиях, когда ядра-излучатели и ядра-поглотители входили в состав кристаллических структур, находившихся при достаточно низкой температуре – был сделан вывод о том, что здесь отдача от гамма-кванта воспринимается не одиночным ядром, а всем кристаллом в целом, становясь при этом, практически, нулевой.
Казалось бы, всё логично? Отнюдь. Наш анализ показал, что в тех самых опытах по «допплеровской компенсации» эффекта отдачи имела место селекция опытных данных: та их часть, которая не согласовывалась с концепцией отдачи от гамма-кванта – несомненно, замалчивалась [Г6]. В лучшем согласии с опытными данными оказывается наша модель [Г6] – согласно которой, резонансному ядерному поглощению в обычных условиях препятствует не «эффект отдачи», а допплеровские смещения, обусловленные тепловыми колебаниями ядер в твёрдых телах. При достаточно низких температурах, когда размах тепловых колебаний ядер становится меньше длины волны гамма-излучения, допплеровские смещения становятся нулевыми из-за эффекта Лэмба-Дика – и имеет место мёссбауэровский режим. Из нашего подхода следует, что, у конкретного кристалла, переход в мёссбауэровский режим для различных длин волн гамма-излучения происходит при различных температурах – а не при одной и той же, дебаевской, как это следует из традиционного подхода. Именно наш подход лучше согласуется с опытом: чего стоит один лишь факт мёссбауэровского поглощения для перехода 14.4 кэВ у железа при температурах вплоть до 1046оК [Н1], хотя дебаевская температура у железа равна 467оК [Ф1]. Кроме того, из нашего подхода следует, что мёссбауэровские ширины определяются не естественными ширинами ядерных линий, а параметрами кристаллической решётки, которая в мёссбауэровском режиме является высокодобротным интерференционным фильтром. Следствием этого вывода является предсказание об анизотропии эффекта Мёссбауэра для монокристаллических образцов – что действительно имеет место [А2,Г7,К3,А3]. Любое объяснение этой анизотропии с позиций традиционного подхода является противоречивым, поскольку здесь для кристаллической решётки подразумевается абсолютная жёсткость, при которой отдача от гамма-кванта воспринимается «всем кристаллом» одинаково во всех направлениях. По совокупности, традиционный подход, в котором гамма-кванты переносят импульс, вновь оказывается неадекватен экспериментальным реалиям.
С началом эры освоения космоса появились, как полагают, свидетельства о том, что давление солнечного света влияет на движение космических аппаратов. Так, в 1960 г. на околоземную орбиту был выведен американский спутник «Эхо-1». В развёрнутом состоянии он представлял собой сферический баллон из майларовой плёнки, металлизированной снаружи. При диаметре баллона 30 м и массе всего 68 кг, спутник имел «большую «парусность» по отношению к давлению солнечного света» [Л4]. За пять месяцев орбита спутника из почти круговой (высота перигея 1520 км, высота апогея 1687 км [К4]) превратилась в эллиптическую (высота перигея 900 км, высота апогея 2200 км [Л4]), за следующие полгода вновь возвратилась к почти круговой, после чего опять стала вытягиваться, и так далее. Торможение о разреженную атмосферу, особенно на перигейных участках, приводило к постепенному опусканию орбиты, и в итоге «Эхо-1» просуществовал на орбите менее восьми лет. Всё выглядело очень похоже на то, что эволюции орбиты «Эхо-1» вызывались действием давления солнечного света [Ш2,М1].
Но мы усмотрели другую причину этих эволюций орбиты – чисто электромагнитную. Ультрафиолетовое излучение Солнца должно было вырывать фотоэлектроны из металлизированной поверхности спутника, заряжая его положительно. Компенсирующий приток электронов из окружающего пространства происходил бы не изотропно: из-за магнитного действия фотоэлектронов, летевших, в основном, в сторону Солнца, притекавшие электроны формировали бы область избыточной концентрации отрицательного заряда с противосолнечной стороны от баллона. Этот избыточный отрицательный заряд притягивал бы положительно заряженный баллон – вот и источник силы, тянувшей его в направлении «от Солнца», когда спутник не находился в тени. Оценки [Г8] показывают: этот механизм вполне реалистичен, поэтому эволюции орбиты спутника «Эхо-1» нельзя считать доказательством того, что их причиной было давление солнечного света.
Далее, после создания узкополосных перестраиваемых лазеров, бурно развивается спектроскопия атомов и ионов, охлаждённых и удерживаемых лазерным излучением (см., например, обзор [Д1]). Лазерное охлаждение атомов и ионов, а также их удержание в оптических ловушках, считаются несомненными свидетельствами передачи этим атомам и ионам импульсов фотонов, которых они резонансно поглощают. Но, на наш взгляд [Г4], здесь происходят совсем иные процессы.
Так, в радиочастотной ловушке ионы совершают колебания в области устойчивого движения. Для лазерного охлаждения облачка ионов, его подсвечивают лазерным лучом, частота которого ниже частоты «охлаждающего» оптического перехода у ионов – с таким расчётом, что ионы, движущиеся навстречу лазерным фотонам, воспринимают их допплеровски увеличенную частоту как резонансную, и эффективно их поглощают. Переизлучение же поглощённых фотонов, как полагают, происходит спонтанно, в произвольном направлении. По этой логике, при поглощении фотонов у иона накапливается тормозящий импульс, а при их переизлучении усреднённый импульс отдачи стремится к нулю – так что колебательные движения иона гасятся, вплоть до эквивалентных температур в сотни и даже десятки микроКельвинов.
Мы же полагаем, что гашение колебаний здесь происходит иначе. Бесспорно, что при поглощении ионом порции световой энергии hf, масса иона увеличивается на величину hf/c2, а при излучении такой же порции энергии, масса иона уменьшается до прежнего значения. Эти повторяющиеся увеличения-уменьшения массы колеблющегося иона могут привести – без какой бы то ни было передачи импульса – либо к параметрическому гашению колебаний иона, либо, наоборот, к их параметрической раскачке. Поскольку нет гарантий, что циклы увеличения-уменьшения массы иона синхронизированы с циклами его колебаний, то ясно, что параметрическое гашение колебаний будет происходить с меньшей вероятностью, чем их параметрическая раскачка. И, действительно, лишь ничтожный процент ионов из облачка испытывает «лазерное охлаждение» - а остальные, наоборот, покидают зону устойчивого движения. Заметим, что параметрическое гашение колебаний у части ионов должно происходить с неменьшим успехом в случае, когда частота лазера выше частоты оптического перехода, т.е. когда резонансно поглощают ионы, движущиеся попутно с фотонами – хотя, согласно традиционной логике, в такой ситуации должен иметь место «лазерный разогрев» ионов.
Ещё один важный экспериментальный результат – это удержание атомов лазерными лучами. Так, в стандарте частоты, называемом «цезиевый фонтан» (см., например, [Д2]), облачко атомов цезия удерживается в «холодном», т.е., практически, в неподвижном состоянии благодаря подсветке, с шести сторон, лазерными лучами, частота которых на ~5 МГц ниже невозмущённой частоты оптического перехода (λ=852 нм) в цезии. Считается, что при движении атома, уводящем его из области перекрестья лучей, он резонансно поглощает фотоны встречного луча и, таким образом, тормозится из-за эффекта отдачи.
Мы же полагаем, что и в данном случае дело заключается не в эффекте отдачи. Находящийся в движении атом воспринимает, из-за эффекта Допплера, частоту встречного луча увеличенной, а частоту попутного луча – уменьшенной. При этом, поразительным образом, искусственно имитируется пребывание атома в условиях градиента частот (2.7), который порождает силовое воздействие, направленное в сторону понижения частот. В результате атом приобретает тормозящее ускорение – как это происходит согласно нашей модели действия тяготения на вещество (2.7).
Добавим, что на том же самом принципе – имитации градиента частот – производится подброс облачка атомов в «цезиевом фонтане». Для этого частоты лазеров, подсвечивающих облачко сверху и снизу, на время порядка одной миллисекунды сдвигают на несколько МГц – частоту подсветки сверху уменьшают, а частоту подсветки снизу увеличивают. В результате этой процедуры облачко атомов, испытавших кратковременную имитацию вертикального градиента частот, начинает свой свободный полёт вверх. Разумеется, традиционный подход объясняет такой подброс облачка атомов иначе – как результат накопления импульсов поглощённых фотонов из подсветки снизу. Для того, чтобы таким способом атому цезия была сообщена скорость в несколько метров в секунду, он должен накопить импульс от ~1000 оптических фотонов – что, за время «подбрасывающего режима», вполне возможно. Но обратим внимание на одно важное обстоятельство. Из опыта достоверно известно, что начальная скорость свободного полёта облачка ионов вверх – по окончании «подбрасывающего режима» - прямо пропорциональна применённой разности частот подсветок снизу и сверху. Между тем, увеличение этой разности частот отнюдь не должно приводить к прямо пропорциональному увеличению числа поглощённых фотонов за время «подбрасывающего режима». Импульсы же этих фотонов, практически, не изменяются при изменении их частоты на несколько МГц. Отчего же усиливается подброс при увеличении разности частот подсветок снизу и сверху? Наше объяснение, через имитацию градиента частот, выглядит предпочтительнее! Похоже, мы имеем здесь дело с парадоксальной ситуацией: экспериментаторы научились искусственно создавать условия, при которых возникает безопорное движение атомов – но, не веря глазам своим, пытаются втиснуть эти результаты в рамки традиционных понятий.
Кстати, нам даже приводили аргументы насчёт давления света, полученные, так сказать, на личном опыте. «Я своей шкурой чувствовал давление света, - рассказывал один. – Был в рубашке, и мне в спину попадали импульсы инфракрасного лазерного дальномера. Каждый импульс отлично чувствовался – не через тепло, а через лёгкое тактильное ощущение!» Неубедительно, профессор! Это тактильное ощущение вызывалось, скорее всего, небольшим местным повышением давления воздуха между спиной и рубашкой – из-за небольшого повышения его температуры. Порог тепловой чувствительности кожи не превышался, а порог тактильной чувствительности – превышался. Вот и всё объяснение. «А ещё, - кричали, - при лазерном воздействии – если мелкий образец не закрепить, то его просто снесёт давлением лазерного излучения!» Друзья, мне самому не чужда тема лазерной обработки материалов. И мне хорошо известно, что из кратера, образуемого лазерным излучением на образце, вылетают, как минимум, продукты испарения материала, а, при неудачно подобранном режиме – ещё и брызги жидкой фазы. Из-за выброса этих масс и возникает «отдача», действующая на образец. Ничего общего с «давлением света» это не имеет.
На основе вышеизложенного, мы не усматриваем экспериментальных свидетельств о том, что фотоны переносят импульс. Что же касается теоретических измышлений – о том, что в звёздах-гигантах свет, идущий из недр, сдерживает их гравитационное сжатие, или о том, что в эпицентре ядерного взрыва давление света так велико, что им и порождается ударная волна – то к этим измышлениям мы не будем относиться серьёзно. Пусть теоретики веруют в давление света. Их так воспитали: когда они были маленькими, им рассказывали сказки про фотонные ракеты. Кто ж виноват в том, что с возрастом они так и не поняли, что это были сказки?
3.3. Опыт Басова: мгновенный переброс лазерного импульса на расстояние.
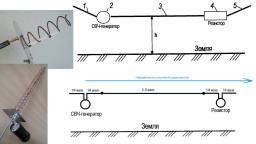
В 1966 г. Басов и сотрудники [Б2] впервые сообщили об эффекте, который до сих пор не имеет разумного объяснения в рамках традиционных физических концепций. Эти авторы исследовали временные задержки на движение лазерного импульса в системе генератор-усилитель. Пара рубиновых стержней-усилителей находилась на расстоянии около 2.5 м от рубинового лазера-генератора. Между генератором и усилителем была установлена делительная пластинка, которая отбирала часть энергии лазерного импульса и направляла её по другому пути, не проходящему через усилитель. Таким образом, лазерный импульс расщеплялся на два, каждый из которых попадал на свой фотодетектор, сигналы с которых подавались на скоростной двухканальный осциллограф. Методика измерений была совсем простой. При выключенном усилителе, т.е. при отключенных лампах его накачки, согласовывали задержки в электрических трактах двух каналов так, чтобы на экране осциллографа оба всплеска фототока происходили синхронно. А потом – повторяли опыт при единственном изменённом условии: при включённом усилителе. И оказывалось, что всплеск фототока от импульса, проходившего через усилитель, теперь опережал во времени другой всплеск, который служил опорным. Изумляла величина этого опережения: она была запредельно велика. Казалось бы: изменения, которые могли уменьшить задержку, происходили лишь на протяжении усилителя. Если допустить немыслимую ситуацию, при которой лазерный импульс проходил бы по включённому усилителю мгновенно, то даже тогда выигрыш во времени составил бы всего около 1.6 наносекунды. А осциллограф чётко показывал: не 1.6, а целых 9 наносекунд! При длительности самого импульса в 3 наносекунды, эффект обнаруживался вполне убедительно – как впоследствии и у других групп исследователей, использовавших среды с различными типами нелинейностей [Ч1,С4,А4,В1].
Мы расцениваем опыт Басова как один из величайших экспериментов ХХ века. Поразительно, как с помощью минимума технических средств можно было получить ошеломляющий результат, который прямо и просто, без всяких кривотолков и «интертрепаций», показал: представления ортодоксальной науки о свете, как о летящих фотонах – причём, летящих со скоростью света – это полная чушь. Проверено: ортодоксы, узнающие про результат Басова, впадают в прострацию и оказываются неспособны сказать по существу ничего членораздельного. Впрочем, были попытки заболтать этот результат и показать, что он «на самом деле ничему не противоречит». Развернулась некоторая деятельность теоретиков, к которой вполне подходит определение «театр абсурда». Ибо теоретики взялись сооружать модели движения лазерного импульса в усилителе со скоростью, превышающей скорость света в вакууме – даже не заикаясь о том, что сама постановка такой задачи повергает в прах специальную теорию относительности (СТО). Вот, например, до чего они додумались (см. обзор [О1]). При движении лазерного импульса в усиливающей среде, коэффициент усиления для переднего фронта импульса больше, чем для заднего, поскольку задний фронт движется по среде, уже частично «высветившейся». Эта неодинаковость коэффициентов усиления приводит к тому, что передний фронт приподнимается над пьедесталом импульса, а задний фронт – приопускается, что в итоге эквивалентно продвижению импульса вперёд по пьедесталу. Складывая скорость движения пьедестала и скорость «усилительного сноса», получали сверхсветовую скорость движения импульса. Самое смешное в этом объяснении было то, что в нём использовалось классическое сложение скоростей, а не релятивистское – которое следовало бы использовать ортодоксам для случая, когда одним из слагаемых являлась скорость света. Куда ж деваться – результатом релятивистского сложения скоростей никак не может быть скорость, большая скорости света в вакууме! Ну, а самое печальное в этом объяснении было то, что оно ровным счётом ничего не объясняло. Во-первых, сокращение времени движения импульса при «включённой» нелинейности в ячейке имело место не только для усиливающих, но, как выяснилось позже, и для поглощающих сред [В1] – лишь бы совпадали спектральные линии у генератора и у нелинейной ячейки. Как интересно: для сверхсветовой скорости лазерного импульса требуется попадание на спектральную линию – как и для сверхсветовой фазовой скорости на линии поглощения в веществе, о чём давно хорошо известно! А, во-вторых, русским же языком было сказано: импульс не просто двигался в ячейке со сверхсветовой скоростью – выигрыш во времени был больше того, каков он был бы при мгновенном прохождении ячейки! Так, в случае, когда роль нелинейной ячейки играла тонкая поглощающая плёнка [В1], обнаруженный выигрыш во времени превышал выигрыш при мгновенном прохождении этой плёнки в 310 раз! Либо этот оглушительный результат негативно сказался на рассудке авторов – ибо они в серьёзном научном журнале заявили о том, что лазерный импульс в нелинейной ячейке движется вперёд по пространству, но вспять во времени: «импульс появляется на выходе ячейки до того, как он входит в неё» [В1] (перевод наш). Либо, будучи в своём обычном рассудке, авторы специально выдали этот абсурд – чтобы зациклить на нём внимание публики, которая иначе зациклилась бы на очевидном крахе СТО. Представляете, на какие жертвы пришлось идти этим авторам, следуя велениям научного долга? Мол, пусть лучше нас считают идиотами или негодяями – лишь бы мы репутацию СТО не подмочили!
И, вот, спрашивается: а стоит ли идти на такие жертвы? Если до такого дошло – не пора ли призадуматься насчёт корректности основных исходных представлений? Не смешно ли ставить задачу так: «Каким образом лазерный импульс проходит по нелинейной ячейке быстрее, чем мгновенно? или, другими словами, каким образом групповая скорость света может быть больше, чем бесконечная?» Может, здесь дело не только в нелинейной ячейке? Ведь во всех подобных экспериментах «выпадающая» задержка – это как раз время, равное расстоянию от генератора до нелинейной ячейки, делённому на скорость света! Во сколько раз это расстояние превышает длину пути света в нелинейной ячейке, во столько раз наблюдаемый выигрыш во времени оказывается больше выигрыша при «мгновенном» прохождении ячейки! О чём это говорит? О том, что когда нелинейность «выключена», лазерный импульс идёт от генератора к нелинейной ячейке со скоростью света, а когда нелинейность «включена», лазерный импульс перебрасывается из генератора в нелинейную ячейку, практически, мгновенно. Тогда мы немедленно получаем идеальное согласие с опытными данными – без насилия над здравым смыслом и без противоречий не только с принципом причинности, но и с элементарными представлениями о движении. Всё в этих опытах становится на свои места; остаётся лишь объяснить – каким образом лазерный импульс перебрасывается мгновенно на расстояние, по крайней мере, в несколько метров.
В рамках традиционных представлений о свете, этот феномен, конечно, не объясняется. По логике же «цифрового» мира, этот феномен совершенно естественен – являясь частным проявлением общего случая распространения света, как цепочки мгновенных квантовых перебросов энергии возбуждения с атома на ато. При этом конечность скорости света, а не её бесконечность, обусловлена конечным быстродействием алгоритма, «прокладывающего путь», по которому производится такая цепочка квантовых перебросов. Этот алгоритм мы называем «навигатором квантовых перебросов энергии».
Полный текст: https://litresp.ru/chitat/ru/%D0%93/grishaev-andrej-aljbertovich/etot-cifrovoj-fizicheskij-mir/3